As people struggle with self-isolation, it’s worth reviewing why we’re doing all this.
Humans aren’t very good at assessing mathematical risk. Our brains aren’t built for it. (See, you were right in high school!)
It takes disciplined effort and training to think statistically or mathematically. These things usually do not match our intuitions.
R-nought
As we discussed in a previous post, the R0 of COVID-19 is probably between 2-2.5. We’ll use 2.3 for ease.
What this means is that each person infected with COVID-19 will, on average, spread it to 2.3 other people during the course of the illness.
All this presumes that no one in the population is vaccinated or otherwise immune.
Well, we have no vaccine. And no one has seen this virus before, so no one is immune. (Over months, most of us will be exposed and become immune–then the same R0 won’t apply, and the epidemic will burn itself out.)
COVID-19 versus influenza
It is common to compare COVID-19 to influenza, and some even complain that we don’t do this kind of hard-core quarantine for influenza.
We do it for a few reasons:
- the entire population is not usually vulnerable to seasonal influenza; there is some immunity;
- the death rate of COVID-19 seems to be much higher than seasonal influenza (probably about 10x higher);
- The R0 for influenza is 1.3.
Is this really a big deal? Is the difference between 1.3 (influenza) and 2.3 (COVID-19) that significant?
Yes.
Brace yourselves, math coming
Influenza example
For an R-nought of 1.3, let’s assume I’m the only person with the disease. How many people will I infect? R0 doesn’t tell us at what rate the disease spreads; it only tells you that over the course of my illness, I’ll give it to 1.3 people on average. (You can’t infect 0.3 of a person obviously; some will infect a few more, some a few less.)
Let’s follow this chain out ten places (me infecting 1.3 people, and each of them infecting 1.3 people, and so on, for 10 “layers”).
That is:
# infected = 1.3 x 1.3 x 1.3 x 1.3 x 1.3 x 1.3 x 1.3 x 1.3 x 1.3 x 1.3
A short hand way to say this is with (shudder!) exponents. Specifically:

Or, “1.3 to the 10th power.” = 13.79, round up to say 14 people.
So I am responsible for 14 infections of influenza if I don’t self-isolate.
COVID-19 example
Now, do the same thing for COVID-19, with an R-nought of 2.3.
Again, let’s assume I’m the only person with the disease. How many people will I infect, again over a chain of 10? (Me and my infections, plus all the infections they cause, 10 times total.
So, that’s 2.3 multiplied by itself ten times, or:

Or, “2.3 to the 10th power” = 4143 (rounded to nearest patient).
So, with the slightly higher COVID-19 R-nought, I am responsible for 296 times more infections (29,600%).
If you assume the higher R-nought is the right number (2.5) then that jumps to 9537 people–681 times more infections (68,100%).
Small shifts in R-nought make a huge difference.
Using graphs
Some people like graphs more. Here’s those two values, plotted on a graph.
The red line is for R-nought=1.3. Notice that at 10 “cycles” out on the horizontal axis, it hits 14.
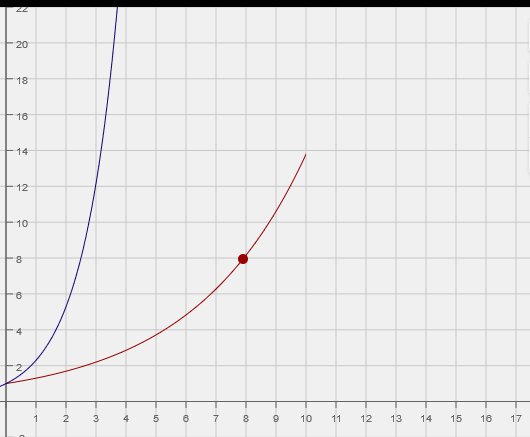
The purple line is for R-nought = 2.3. Notice that within 4 cycles, you’ve already infected more people than 10 cycles of 1.3. And, it just explodes upward–that purple line won’t reach 10 until it is up beyond 4000 on the vertical axis.
Now this is an over-simplification. There are lots of other factors. And, as more people are infected, this becomes less the case.
But it gives you a back-of-the-envelope sense of the type of problem we’re facing.
Why this matters
So, this explains why we’re self-isolating. It’s to try to keep that R-nought value down. Self-isolating reduces the number of people you will infect (hopefully to zero, but certainly lower).
If we don’t control R-nought, then all these people will explode with illness at once. And there’s no way we can cope with even the small fraction who get seriously ill. We have to slow it down so R-noughts are more like influenza (which will strain us, but which we can and do handle every year).
This also explains why “cheating” on your social isolation is such a bad idea. (“I’m just going to see my friends for a minute; we’re just going to run over to grandma and grandpa’s house once.”)
No. Just, no.
All you need to do is infect one more person than you otherwise would, and you’ve completely negated any benefit from your isolation. If you infect 2 people instead of 1 person, or 3 instead of 2, you’ve increased the disease massively if everyone else is behaving as you are.
(Don’t use this as an excuse to chuck your isolation if you’ve already cheated–remember, these numbers are averages, and so some people will do more than 2.3. Don’t be that person! Don’t make previous mistakes worse.)
But, these facts should make an overwhelming problem seem manageable. All you have to do is avoid infecting someone. Even if you avoid only one infection, that has a massive add-on effect, and you’ve made a real contribution. By contrast, if you don’t avoid one infection, you’ve caused massive amounts of damage.
Some infections will have bigger impacts
Plus, if you infect someone in a critical position–like a doctor or nurse–then your impact becomes even greater because that person doesn’t just become another sick case and potential hospital user. It also takes them out of the caring for others.
(This is why I decided I was keeping my kids home from school even before the province announced it. I didn’t want them to spread it, but more importantly I knew that if they spread it to me, that would have a higher “cost” to others.)
Conclusion
So, don’t cheat. Don’t make exceptions. Ignore your kids when they complain. Don’t think you’re special. You’re not.
Math plays no favourites.
